Sommerfugleeffektens fader død

Først i 1920'erne blev opfattelsen ramt af et mindre jordskælv, da kvantemekanikken blev formuleret og introducerede hidtil utænkelige begreber: Hændelser kan ikke forudsiges helt eksakt. Det skær af tilfældighed, som f.eks. partiklers henfald må beskrives med, behagede ikke datidens videnskab. Einstein, der gik ud fra, at alt virker på alt og dermed kan forudsiges, mente, at man enten måtte skippe kvantemekanikken eller relativitetsteorien for at kunne forsvare et forståeligt virkelighedsbillede. Senere, men aldrig i de to fysikeres levetid, skulle det vise sig, at på dette punkt var det Bohr, der fik ret overfor Einstein.

Indtil kvantemekanikken blev indført, havde et af de vigtigste videnskabelige aksiomer antaget, at lige påvirkninger giver lige udfald. Ellers ville ingen videnskabelig læresætning have nogen almengyldig virkning. I den klassiske naturvidenskab udvider man endog begrebet og antager, at næsten ens påvirkninger giver omtrent ens udfald.

I de fleste tilfælde er det både nødvendigt og fornuftigt at være large overfor små forstyrrelser. Ellers ville det ikke være muligt at bygge funktionsdygtige maskiner, da selv ikke den mest minutiøst udførte eksperimentielle opstilling er fri for ydre påvirkninger. Erfaringen med, at tilstande i vor omverden kan forudsiges, er grundlaget for overlevelse på vor planet.

Men eksperimenter viser igen og igen, at det ikke altid er muligt at forudsige ting. I 1963 fodrede meteorologen Edward Lorenz sin Royal McBee med en vejrmodel. Da han senere fodrede computeren med et afrundet mellemresultat, han tidligere var nået frem til, for endnu en gang at regne på vejrmodellen, var resultatet forbløffende: Computeren spyttede værdier ud, der end ikke mindede om første forsøgs udfald. Lorenz drog den korrekte konklusion og forsøgte ikke at give computerens manglende regnenøjagtighed skylden, eller at skyde skylden på det faktum, at hans computer var bygget af radiorør og derfor brød sammen en gang om ugen. Han så i stedet, at mellemresultatet havde været ubetydeligt afrundet og forstod, at hvis atmosfæren forholder sig på samme måde, er en langtidsprognose umulig.

Lorenz kaldte dette fænomen for sommerfugleeffekten: Selv hvis atmosfæren rettede sig efter en deterministisk model, hvor alle indflydelsesfaktorer var kendte, kunne selv vingeslaget på en sommerfugl ændre vejret på længere sigt. Videnskaben kunne ikke længere tro på Newtons og Laplaces vision om, at forudsætningen for præcise forudsigelser blot lå i tilstrækkeligt præcise målinger. Man måtte indse, at uorden, tilfældigheder, irregulære forhold - eller kort sagt "kaos" - afløste ordenen.

Videnskaben stod uforstående overfor de nye iagttagelser, men det skulle snart vise sig, at kaos og orden gik hånd i hånd.

Biologen Robert May undersøgte en simpel vækstmodel for populationer, der var udformet således, at kraftige udslag blev dæmpet. Han ændrede en parameter i vækstmodellen og så, at populationen, der hidtil havde været stabiliseret, pludselig svingede mellem to værdier. Ændrede han igen parameteren, svingede populationen mellem 4, 8, 16... indtil man pludselig ikke kunne forudsige perioden, og systemet ikke var blevet mangedoblet, men kaotisk. Så man nærmere på systemet, kunne man imidlertid også se tydelige perioder af orden midt i kaos.

Mitchell Feigenbaum så nærmere på dette og andre oscillerende systemer, og nåede frem til den konklusion, at der i alle kaotiske systemer tilsyneladende opstår orden i uordenen, samt at der altid kan opstå kaotiske systemer af oscillerende feed-back systemer gennem den periodedobling, som May havde analyseret - i hvert fald hvad matematiske systemer angår. Senere skulle forsøg foretaget af Harry Swinney vise, at turbulens i væsker også skifter fra frekvensdobling til kaos, og målinger foretaget på MIT viste, at også i optagten til hjerteslag kunne periodedobling iagttages. Feigenbaums beregninger viste, at forholdet mellem alle disse oscillerende systemers periodefordoblinger var den samme; en tilsyneladende universel konstant på ca. 4,67, der fortjener betegnelsen naturkonstant. Feibenbaum fandt således en matematisk beskrivelse for kaos.

Mere kendt er dog Beniot B. Mandelbrot, hvis grafiske modeller udtrykte samspillet og sammenhængen mellem kaos og orden på en måde, der fik selv ikke-matematikere til at spærre øjnene op i forundring. Mandelbrot var på det tidspunkt ansat ved IBM, hvor han studerede transmissionsstøj i selskabets telefonlinier. Han lagde mærke til, at støj kom i "klumper", dvs. der kunne komme en periode uden støj efterfulgt af perioder med støj. (Dette er et velkendt statistisk fænomen, som dybest set handler om, at hvis tilfældigheder opstod i form at et fast, gentagende mønster, ville det jo netop ikke være nogen tilfældighed.) Inddelte han støjperioderne, så han, at disse igen var opdelt i nye perioder, der endnu engang var opdelt i perioder, og så fremdeles. Denne mængde var en Cantor-mængde (efter matematikeren Georg Cantor), der nu viste sig ikke blot at eksistere som et abstrakt, matematisk begreb, men også som et naturligt observerbart fænomen.

På denne måde kom Mandelbrot, ligesom Lorenz, til at tænke på, at naturen måske kunne rette sig efter en anden geometri end den årtusindgamle euklidske. Den euklidske geometri kunne nemlig ikke beskrive brudte, uregelmæssige former, som Mandelbrot døbte "fraktaler" efter det latinske "fractus".

Den euklidske geometri går ud fra, at alle figurer har dimensionerne 0, 1, 2 eller 3 som funktion af målene længde, bredde og højde. Men en "figur" som en kystlinie har ingen bestemt længde. Jo tættere, man er på, desto flere bugter og vindinger ser man. Kysten bliver længere, desto tættere, man kommer på. Man forstår, at går man uendeligt tæt på, er kysten uendeligt lang. Det er med andre ord umuligt at måle længden entydigt. Det eneste, der holdes konstant, når man går tættere på eller fjerner sig fra kysten, er kystens grad af ujævnhed. Denne ujævnhed viste Mandelbrot, at man kunne beskrive som ikke-heltallige dimensioner, idet en kystlængde f.eks. kunne være 2,3-dimensionel i stedet for 2-dimensionel, hvilket i en intuitiv forstand antyder, at den til dels udfylder et 3-dimensionelt rum, men dog stadig mest minder om en kurve. Alle de figurer, som Mandelbrot beskrev med disse brudte dimensioner, havde en fællesnævner: Ligegyldigt, hvor tæt man zoomede ind på figurerne, mindede de på en eller ande måde om sig selv - de var selvsimilære.

I de matematiske systemer, der udviste orden og kaos blandet i form af selvsimilaritet og brudte dimensioner, begyndte matematikerne at operere med begrebet attraktorer. En attraktor er fraktalgeometriens svar på et "fixpunkt", dvs. det resultat - et tal eller en ny matematisk funktion - som en itereret funktion (dvs. en funktion, der gentages igen og igen, idet man for hver gentagelse benytter funktionens resultat som input), altid vil nærme sig, eller som den itererede funktion alternativt altid fjerner sig fra. Som navnet antyder, er en attraktor noget, som den matematiske funktion bliver "trukket imod". Det kan være et simpelt tal, men kan også være en række punkter eller en "figur". For de kaotiske systemers vedkommende blev mønsteret for deres indbyggede orden omtalt som strange attractors - "mærkelige" attraktorer.

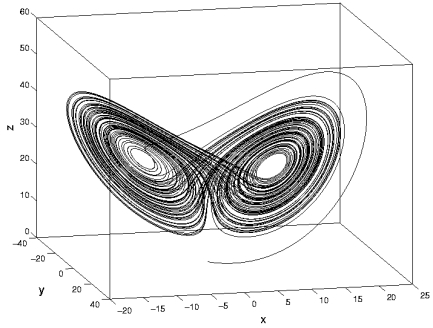
Lorenz-attraktoren har de typiske træk for en attraktor: Itererer man på et punkt, der ligger udenfor attraktoren, bliver det suget ind i attraktoren, uanset hvor det lå. Herefter vil det løbe langs de linier i attraktoren, som man ser i figuren. I Lorenz' vejrmodel ville et punkt udenfor attraktoren svare til snevejr i Sahara, hedebølge på Nordpolen eller andre usandsynlige hændelser. Skulle de forekomme, ville de hurtigt fortage sig og blive trukket ind i attraktoren, dvs. det "normale" klima igen.

Fraktalgeometrien, og ikke minst Lorenz' opdagelse, bør give stof til eftertanke. Modeller, der benytter sig af fraktalgeometri, lader på overbevisende vis naturen beskrive langt bedre end den sædvanlige euklidske geometri ud fra den simple betragtning, at alle figurer af sin type i naturen på den ene eller den anden måde ligner hinanden og, når man går tæt på, også ligner sig selv.

Kaosteorien - fællesmængden for alle disse iagttagelser - har ikke løst problemet med forudsigelse, tværtimod. Den fortæller os, at selv ikke hvis vi kender et kaotisk system til bunds, er det muligt at forudsige komplekse systemer som f.eks. klimaet på længere sigt. Hvad kaos kan lære os er grænserne for forudsigelse - hvornår en prognose bliver usikker.

Desuden kan kaosteorien lære os at være på vagt overfor vore handlinger. Det nuværende klima er dannet af forskellige faktorer såsom temperatur, mængden af forskellige gasarter i atmosfæren, corioliskraften, etc. Vore huller i ozonlaget, udledning af CO2 og andre påvirkninger af naturen kan, i følge sommerfugleeffekten, til syvende og sidst påvirke vejret i en sådan grad, at det springer til en ny attraktor - i dette tilfælde til et andet klima, hvilket ville svare til en naturkatastrofe af hidtil ukendte dimensioner.